Revisiting LCOM

Revisiting LCOM
by Tushar
in Research

tagged Cohesion, LCOM, OO Metrics, CK Metrics

Check out my post YALCOM and our paper for more refined information, experiments, and results.

Along with other metrics, LCOM (Lack of Cohesion in Methods) was first defined by C&K in the OOPSLA paper [1] that invented a new field of object-oriented metrics. LCOM shows the degree of lack of cohesion among methods of a class. In other words, it reveals the extent to which methods of a class works towards realizing a single responsibility. It is an important measure because it indicates whether the present set of methods should be together in a class or could be split to form two or more cohesive classes.

Have you come across a situation when the value of LCOM for a class shows a number that indicates the class is not cohesive but a manual look reveals a different story? Such an instance make you disbelieve the value provided by the metric in general. Recently, I fell in the above situation which makes me perform the following experiment.

There are many definitions of LCOM [1, 2, 3, 4, 5] and the value we get depends on what method our static analysis or metric tool is using. In this experiment, I computed LCOM values based on different methods for three small cases and compare whether they match our perceived notion of cohesion.

Let me first present three examples that I am using for this experiment. I have a set of methods M1, M2, … and a set of instance variables V1, V2, … An edge between a method and a variable shows an access from the method to the variable.

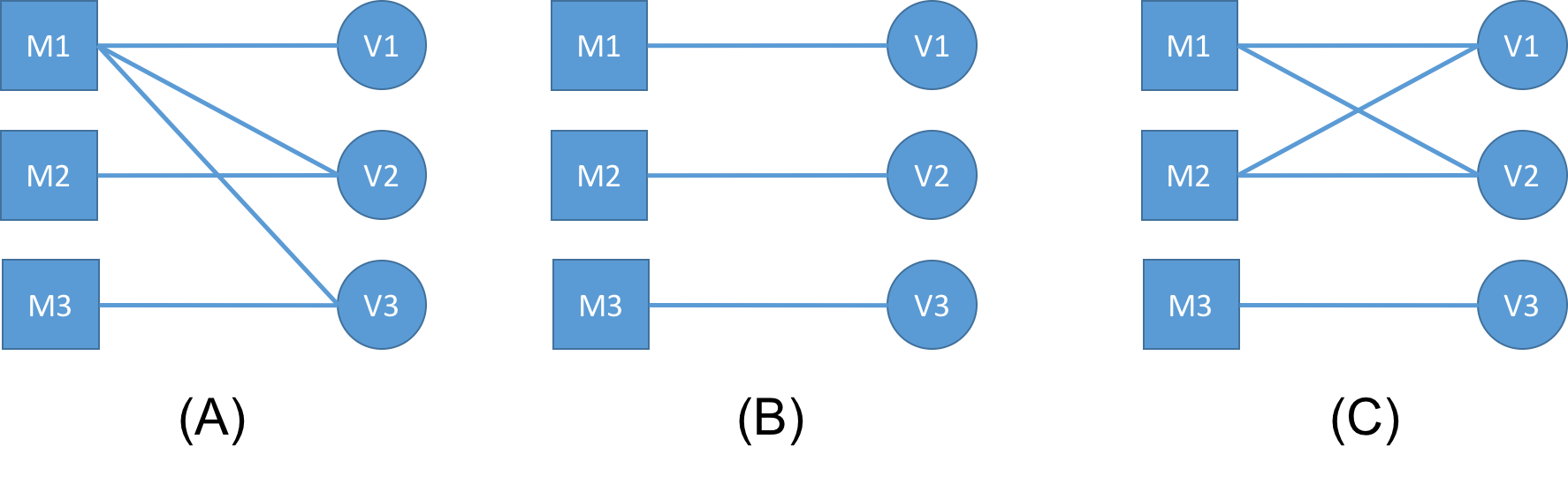Running examples Running examples of the experiment

Class shown in case (A) could be considered cohesive, case (B) shows an extreme case of a non-cohesive class, and the class in case (C) is non-cohesive.

LCOM definitions

In this section, I am reproducing various definitions of LCOM. Although, some researchers differentiated LCOM definitions by LCOM1, LCOM2, and so on, there is an inconsistency in such a tagging (i.e., some researchers refer original definition of C&K LCOM defined in 1991 as LCOM1 while some refer C&K definition of LCOM appeared in 1994 as LCOM1). Therefore, to avoid confusion, I am referring LCOM definitions by the year in which they published.

  1. LCOM91: It is defined by Chidamber et al. [1] as follows:
    Consider a class C1 with methods M1, M2…Mn. Let {Ii} = set of instance variables used by method Mi. There are n such sets {I1},…{In}.
    LCOM = the number of disjoint sets formed by the intersection of the n sets.
  2. LCOM94: It is defined by Chidamber et al. [2] as follows:
    Consider a class C1 with n methods M1, M2,…Mn. Let {Ii} = set of instance variables used by method Mi.
    There are n such sets {I1}, …{In}. Let P = {(Ii, Ij)|Ii ∩ Ij = ∅} and Q = {(Ii, Ij)|Ii ∩ Ij ≠ ∅}. If all n sets {Ii},…{In} are ∅ then P = ∅.
    LCOM = |P| - |Q|, if |P| > |Q|
    = 0 otherwise
  3. LCOM93: It is defined by Li et al. [5] as follows:
    LCOM = number of disjoint sets of local methods; no two sets intersect; any two methods in the same set share at least one local instance variable; ranging from 0 to N; where N is a positive integer.
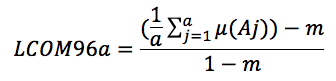
  4. LCOM96a: It is defined by Handerson et al. [3] as follows:LCOM96a
    where a and m are number of attributes and methods respectively, and μ(Aj) is the number of methods accessing attribute Aj.
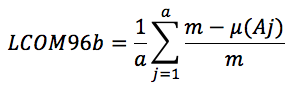
  5. LCOM96b: It is defined by Handerson et al. [3] as follows:LCOM96b
    where a and m are number of attributes and methods respectively, and μ(Aj) is the number of methods accessing attribute Aj.
  6. LCOM95: It is defined by Hitz et al. [4] as follows:
    Let X denote a class, Ix the set of its instance variables of X, and Mx the set of its methods. Consider a simple, undirected graph Gx(V, E) with
    V = Mx and E = {<m,n> ∈ ∃ VXV | iIx: (m accesses i) ^ (n accesses i)}
    LCOM(X) is then defined as the number of connected components of Gx (1≤ LCOM(X) ≥ |Mx|).

Results

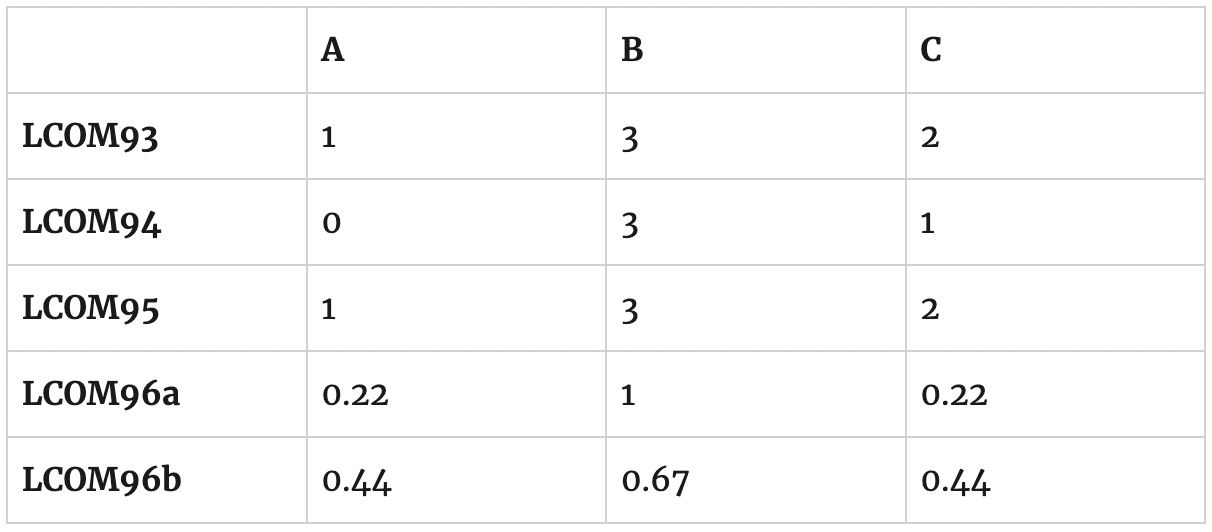
The following table shows computed LCOM for all three cases using the above described methods.

LCOM results

LCOM96a and LCOM96b are popularly used LCOM definitions (for instance, NDepend and Designite implement one of the variants). However, both of them show same LCOM value for case A and C! Class shown in case A looks more cohesive than case C. Thus if an LCOM method shows same values for both the cases, the method has a deficiency to capture the cohesiveness of a class.

Results produced by methods LCOM93 and LCOM95 are same and closer to my expectation. On the other hand, these methods do not produce normalized values.

LCOM17

Well, allow me to present a yet another LCOM computation method. It is a scaled and normalized version of LCOM95. To compute an LCOM value based on LCOM17, we need to follow the following steps:

  1. Compute an LCOM value using LCOM95.
  2. Offset the result of LCOM95 by -1 (since the minimum value that LCOM95 produces is 1).
  3. Normalize the result obtained in step 2 (by dividing the outcome of step 1 by number of attributes in the class). The result is a normalized [0,1] value of LCOM.
  4. In case, the number of attributes in the class is zero, then I would prefer to say that the LCOM cannot be computed for the class rather than assigning 0 (perfectly cohesive class).

Intuitively, this method looks good to me. A rigorous experiment is required to prove its correctness in various scenarios.

Challenges with LCOM computation

  • Dependence on method-attribute access: The present set of LCOM computation methods uses common attribute accesses from methods as a basis to decide whether two methods are cohesive. There are situations when this strategy doesn’t work; for example, a utility class has methods to read and write data from files and doesn’t declare any attribute. In this case, the present set of methods will produce either a 0 or a non-deterministic value.
  • Getters/Setters: If an LCOM computation method includes getters and setters in the analysis and treat them as methods, the result will be skewed towards low cohesion. Such inclusion is not a good idea since, by definition, getters and setters only access one attribute and thus will produce an LCOM value showing lower cohesion.
  • Hierarchy: Yet another challenge in LCOM computation is concerning to attributes that are present in the base class but only accessed by its derived classes. For methods in the derived classes, the common access to such an attribute is not considered by most of the present methods. Although the issue has been discussed in a few research papers [6], the present set of tools has not adopted it widely.

References

  1. Chidamber, S. R., & Kemerer, C. F. (1991). Towards a metrics suite for object oriented design (Vol. 26, pp. 197–211). Presented at the OOPSLA '91: Conference proceedings on Object-oriented programming systems, languages, and applications, New York, New York, USA: ACM. http://doi.org/10.1145/117954.117970
  2. Chidamber, S. R., & Kemerer, C. F. (1994). A metrics suite for object oriented design. IEEE Transactions on Software Engineering, 20(6), 476–493. http://doi.org/10.1109/32.295895
  3. Henderson-Sellers, Brian, Larry L. Constantine and Ian M. Graham. “Coupling and cohesion (towards a valid metrics suite for object-oriented analysis and design).” Object Oriented Systems 3 (1996): 143-158.
  4. Hitz, Martin and Montazeri, Behzad. “Measuring coupling and cohesion in object-oriented systems”. Proceedings of International Symposium on Applied Corporate Computing (1995): 25-27.
  5. W. Li, S. Henry. “Maintenance Metrics for the Object Oriented Paradigm”. In Proc. 1st Int. Software Metrics Symp., Los Alamitos, CA, May 21-22 1993, IEEE Comp. Soc. Press, 1993, 52-60.
  6. Etzkorn, Letha and Davis, Carl and Li, Wei. “A Practical Look at the Lack of Cohesion in Methods Metric”. Journal of Object-oriented programming, 1998, vol. 11, no 5, 27-34.